2x2 Rubik's cube solver


Introduction
This program solves a given 2x2 Rubik's cube and displays the solution in chunks of four moves at a time.
It should be noted that the solver will produce solutions that are much longer than necessary, due to the simple algorithm chosen.
The basic theory behind the approach comes from this document.
Code snapshot for this article (tagged rubik2x2-2018-05-12): .zip, .tar.gz. For latest version, go to the github page.
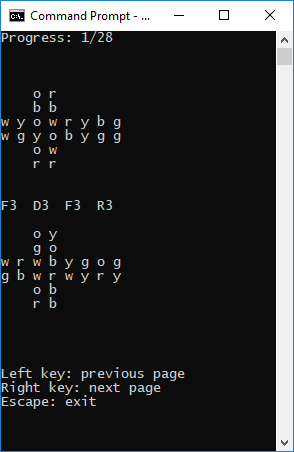
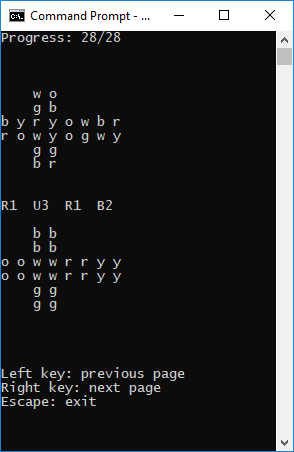
Command line interface
Below is an example command line.> rubik2x2 w=front r=right b=up o=left y=back g=down left{w,w,g,y} right{y,y,b,r} down{r,r,o,w} up{o,r,b,b} back{g,g,g,b} front{y,o,o,w}
First, an alias for each side is set up. I use the first letter of a color as alias for the corresponding side: orange, red, green, blue, yellow, white. This is done so that the colors don't need to be translated to sides when entering the state of the cube.
Then follows the specification of the state of the sides. Here the aliases we just specified are used inside the curly brackets. left{w,w,g,y} means that we're specifying the left side side aliases (colors) as white, white green and yellow. But in what order? The order is: primarily move from low to high values in x direction, secondarily in the y direction and tertiarily(?) in the z direction.
Algorithm overview
The basic algorithm is based on two simple macros. The first macro swaps the positions of two cubies, ignoring orientations. The second macro twists (changes orientation) of two cubies by one step in opposite directions, keeping positions of all cubies fixed. These two macros can be generalized such that they will swap positions or change orientations of any two cubies.
The algorithm proceeds by decomposing the state of the cube into a position permutation, and a set of orientations of the cubicles.
Then, the position permutation is decomposed into transpositions. The first macro may then be used to invert each of the transpositions. That means that the resulting cube will have all cubies in the right positions, but not necessarily in the right orientations.
Finally, we apply the second macro to twist the left-down-back and any other cubie. That means we can twist any cubie which is not left-down-back by any amount, which means we can twist those cubies to their correct orientation. But it's a known fact (see the document) that the sum of orientations modulo 3 is always 0. Therefore, the left-down-back cubie must have an orientation of zero as well, and so the cube is solved.